Abstract

In the present paper, in order to clarity the effects of non-Newtonian liquid properties on the flow, similar experiments have been conducted for that of 0.4 wt% polyacrylamide (PAM) aqueous solutions as the working liquid, and air as the working gas. Liquid single-phase and air-liquid two-phase flow experiments were conducted at room temperature using the horizontal rectangular mini-channel with a sudden expansion. The cross-sectional dimensions of the narrow channel upstream from the sudden expansion were 2.79 mm, 3.09 mm and 2.94 mm in the height (H), the width (W) and the hydraulic diameter (DH), while those for the wide channel were 2.95 mm, 5.98 mm and 3.95 mm. The pressure distributions in the channels upstream and downstream from the expansion were measured with calibrated pressure transducer to determine the pressure change due to the expansion. The flow pattern, the bubble velocity, the bubble length, and the void fraction were measured with a high-speed video camera. The flow pattern map is drawn from the observed flow pattern, i.e., bubble flow, slug flow and annular flow in both the wide and the narrow channels. The bubble length data were compared with the calculation by the scaling law proposed by Kanezaki et al. and Kawahara et al. The pressure change data at the expansion were compared with our previous data together with several correlations in literature. Results of such experiment and comparisons are reported in the present paper.

Keywords

Non-Newtonian, Two-Phase Flow, Sudden Expansion, Minichannel

Share and Cite:

Received 31 July 2016; accepted 26 August 2016; published 29 August 2016

1. Introduction

Two-phase flows across singularities such as bend, contraction and expansion are commonly seen in piping of many industrial systems and/or devices. Recently the emergence of the micro chemical technology demands high efficient reactors with more compact structure, which have to consider gas/non-Newtonian fluid two-phase flow in micro- or mini-channels [1] . A number of researches have been reported on two-phase flows in small channel with singularities. Among them, Sadatomi et al. [2] investigated flow regime, pressure drop, bubble velocity and void fraction for air-water two phase flow through U-bend, sudden expansion and sudden contraction in rectangular minichannel. Kawahara et al. [3] conducted experimental investigations on gas-liquid two-phase flows in two kinds of rectangular microchannels with the width of in the larger channels upstream from the contraction were 0.53 or 0.78 mm at 0.230 mm in height, while that in the smaller ones was 0.270 mm at 0.230 mm in height. To know the effects of liquid properties, the test liquids were changed as distilled water, ethanol 49 wt% aqueous solution, pure ethanol and Hydrofluoroether (HFE)-7200 while the test gas was fixed as nitrogen gas. Abdelall et al. [4] performed an experimental study of pressure drop cause by abrupt flow area changes in small circular channels. The larger and smaller tube diameters were 1.6 and 0.84 mm, respectively. Deionized water and air were used as two-phase flow mixture. Chen et al. [5] conducted experimental investigation of the two- phase flow characteristics across sudden contraction using air and water mixture. The contraction test section was from small rectangular channels of 3 × 6 mm and 3 × 9 mm to a small circular tube of 3 mm i.d. Padilla et al. [6] conducted experimental studies on two-phase flow of HFO-1234yf, R-134 and R-410A in a 10 mm glass tube with a cross-section area ratio of 0.49. The experimental pressure drop data were used to test six prediction methods from literatures.

However, as far as we know the studies on gas and non-Newtonian liquid two-phase flows across singularities in minichannel are still limited. Non-Newtonian fluids, such as paint, milk, toothpaste, animal blood, etc. are ubiquitous in nature, and they are often encountered in many industries, like in chemical engineering, bio-che- michal engineering, food processing, oil exploration, and medical engineering [7] . Fu et al. [7] observed the flow patterns of Newtonian/non-Newtonian fluids two-phase flow in T-shaped rectangular microchannels by using a high-speed camera. Three different dimensions of microchannels were employed with 400 μm × 400 μm, 400 μm × 600 μm, and 400 μm × 800 μm in depth and width, respectively. The cyclohexane was used as the dispersed phase, and various concentrations of Carboxymethyl Cellulose (CMC) aqueous solutions as the continuous phase. Link et al. [8] realized a numerical investigation of an elasto-viscoplastic thixotropic fluid flowing through a 1:4 plane expansion using a recently proposed constitutive equation. The conservation equations were solved using a four-field Galerkin least-squares formulation in terms of the extra stress, pressure, velocity, and structure parameter, i.e., a scalar quantity that represents the structuring level of the material microstructure. The focus is on determining the effect of thixotropy, elasticity and viscoplasticity on the topology of yielded and unyielded regions of the expansion, on the field of structuring level, and on the field of elastic strain.

Li et al. [9] developed a model which predicts liquid holdup (ε_TPL), pressure gradient and frictional multiplier (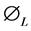) for non-Newtonian liquid-gas flow with different interfacial shapes. The interfacial shape was calculated by solving the Young-Laplace equation, by assuming the non-Newtonian liquid as a power-law shear-thinning liquid. The results showed that the interfacial shape can be assumed as an arc shape when Bond number was lower than 10. The model can predict liquid holdup, two-phase pressure gradient and frictional multiplier for uniform stratified flows. The result also indicates that the interfacial effects on the holdup and pressure difference between two phases were significant, especially for small liquid holdups. Picchi et al. [10] studied flow pattern transition, pressure gradient, hold-up predictions in gas/non-Newtonian power-law fluid stratified flow. Pressure gradient and hold-up were predicted by two different theoretical approaches: the steady fully developed two-fluid model and the pre-integrated model. The theoretical predictions were compared with experimental data available for horizontal and for slightly downward inclined air/shear thinning fluid stratified flow taken from literature. The predictions of the pre-integrated model were validated showing a good agreement when compared with experimental data. Tang et al. [11] conducted experimental investigations on single-phase non-New- tonian liquid flow in microchannels. Experiments were conducted using deionized water and the PAM solution over a wide range of Reynolds numbers as the test liquids and fused silica microtubes with diameters from 75 to 250 μm, fused silica square microchannels with equivalent diameters of 75 and 100 μm, and stainless steel microtubes with diameters from 120 to 300 μm as the test channels. They obtained mass flow rate and friction factor data for deionized water in smooth fused silica microchannels, and the data were in good agreement with theoretical predictions for conventional-sized channels while the deviation was observed for the data in stainless steel microtubes due to the roughness.

Mansour et al. [12] performed an experimental study of non-Newtonian two-phase flow through microchannel having hydraulic diameter of 0.25 mm as the test channel. Distilled water, and 3 types of polyacrylamide aqueous solutions (PAM 0.1 wt%, PAM 0.2 wt% and PAM 0.4 wt%) were used as working liquids, while nitrogen gas as the working gas. The pressure drop data can be accurately predicted by Lockhart-Martinelli method with a newly developed two-phase friction multiplier as function of void fraction and rheological flow index. Yang et al. [1] conducted experimental investigation on nitrogen/non-Newtonian fluid two-phase flow in vertical noncircular microchannels. Square and triangular cross-sectional channels with 2.5, 2.886 and 0.866 mm in hydraulic diameters were used. Three non-Newtonian aqueous solutions with typical rheological properties, i.e., 0.4% Carboxymethyl Cellulose (CMC), 0.2% Polyacrylamide (PAM) and 0.2% Xanthan Gum (XG) were chosen as the working fluids. The rheological properties of the non-Newtonian fluids and geometrical factors were found to affect flow pattern transitions. Goto et al. [13] investigated pressure drop for gas and PAM 0.4 wt% liquid two-phase flows through sudden expansion in horizontal rectangular minichannel. The experimental data on pressure change at the expansion were compared with the some literatures.

Recently, Santoso et al. [14] - [16] in our group have investigated two-phase flow characteristic in rectangular minichannel with sudden expansion and sudden contraction in a horizontal plane. The cross-sectional sizes of the channel were from 3.09 mm by 2.79 mm to 5.98 mm by 2.95 mm for the sudden expansion and vice versa for the sudden contraction. They used water and viscoelastic liquid of 0.1 wt% PAM aqueous solution as the working liquid, while air as the working gas.

In the present study, following to Santoso et al.’s studies mentioned above, experiments have been conducted with air and PAM 0.4 wt% as the working fluid and the same rectangular minichannel with the area ratio of σ_A = 0.49 as the test channel. The objective of the present study is to clarify the effects of non-Newtonian viscoelastic liquid on the characteristics of flow through sudden expansion for both single-phase and two-phase flows. Data for the experimental results obtained from air-PAM 0.4 wt% system will be compared with previous data for air-water and air-PAM 0.1 wt% flow and those from the other researchers in literatures.

2. Experiments

A schematic diagram of the test facility in the present study is shown in Figure 1, being the same as that used in our previous study [13] - [16] . Pressurized air from a compressor pushed the test liquid in a tank and supplies it to the test channel. Thus, no mechanical pump was used in the present experiment to avoid pulsation by the pump and also to avoid contamination by the pump. Figure 2 shows a schematic diagram of test channel with sudden expansion placed on a horizontal plane. The test channel had a rectangular cross-section and made of transparent acrylic resin for visual observation. The port #1 was the liquid inlet port, while the port #2 was the gas inlet ports. Therefore, two phases were supplied through the section 1 as a gas-liquid mixer.

The port #6 was the gas-liquid mixture outlet to atmosphere. The port #3, #4 and #5 were closed in the present experiment. It is noted that if port #4 and #6 were used as the inlet ports of gas and liquid, and port #5, #2 and#3 were closed, the sudden contraction test can be conducted with the same test channel. P₁ to P₁₂ were the pressure taps, and the pressure at P₄ was measured with a gauge type pressure transducer (Yokogawa, FP101-L31-L20). The pressures at other pressure taps were determined from the difference in pressure between the respective taps and P₄ tap measured with a differential pressure transducer (Validyne, DP15-32 or DP15-26 depending on the pressure range). The accuracy of the pressure measurement was within 3.5 Pa from a calibration test.

Volume flow rate of air was measured with a flow meter (KEYENCE, FD-A10 or FD-A1 depending on the flow rate range) within 2%, while that of water with a flow meter (KEYENCE, FD-S) within 1%. In order to obtain accurate time averaged values of air and water flow rates and pressures, the output signals from the respective sensors were fed to a personal computer via A/D converter over 10 sec. usually at 1 kHz.

Table 1 shows the cross-sectional dimensions of the test channel. The width (W), the height (H) and the hydraulic diameter (D_H) for the wide channel were 3.09 mm, 2.79 mm and 2.94 mm, while those for the narrow channel were 5.98 mm, 2.95 mm and 3.95 mm, thus the area ratio σ_A is about 0.49. In this study, water and aqueous solution of 0.1 wt% and 0.4 wt% polyacrylamide (PAM) were selected as the working liquid, while air as the working gas at room temperature. Polyacrylamide aqueous solution is known as a kind of non-Newtonian fluid having viscoelasticity dispensable [17] . Also, PAM aqueous solution has shear thinning effect where the apparent viscosity decreases with increasing of the shear rate and is often expressed by the Ostwald-de Waele power law model as follows:

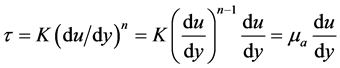(1)

where 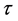is the wall shear stress, is the shear rate, K is the consistency coefficient, n is the flow index and 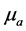is the apparent viscosity. In this study, the values of K and n were determined with a capillary method [18] . The n and K determined as well as the density, the surface tension for the test liquids used in the present and the previous studies are listed in Table 2. n for both water and PAM aqueous solution were investigated within the share rate range of 80 to 12000 1/s.

For single-phase flow experiments, the ranges of Reynolds number (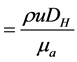, u where is the mean velocity,

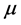the apparent viscosity) in the narrow channel Re_N are from 320 to 9600 for water, and from 290 to 5900 for PAM aqueous solution. For two-phase flow experiments, the ranges of volumetric fluxes of liquid and gas are 0.1 < j_L < 2.3 m/s and 0.1 < j_G < 10 m/s.

3. Result and Discussion

3.1. Data Reduction

Figure 3(a) and Figure 3(b) show examples of pressure distribution data obtained for a PAM 0.4 wt% single-phase flow and an air-PAM 0.4 wt% aqueous solution two-phase flow. The ordinate is the gauge pressure, while the abscissa is the distance from the singularity. The total pressure change across sudden expansion, ∆p_e,

was determined by the extrapolations of the axial pressure profiles upstream and downstream from the expansion. ∆p_e consists of the irreversible and reversible pressure drop, and could be expressed by the following Kays’s equation (Kays, [19] ):

(2)

(3)

where ρ is the density of the working fluid, the mean velocity in the narrow channel, K_e the expansion loss coefficient, the cross section area of the narrow channel, the cross section area of the wide channel and the area ratio.

In order to check the accuracy of the pressure measurement, the single-phase friction factor data were determined from the fully developed pressure gradient data in the upstream and the downstream channels. Figure 4(a) and Figure 4(b) show the Darcy friction factor data, respectively for the channels upstream and downstream of the singularity. The data are plotted against the Reynolds number, based on the hydraulic diameter. The present data in turbulent flow are compared with calculated curve by Sadatomi et al. [20] , while those in laminar flow with calculated curve by Shah and London [21] which is a function of aspect ratio, , for rectangular channels:

(4)

Most data beside the data of PAM 0.1 wt% in laminar flows agree very well to the two curves, and the accuracy of pressure measurement in the present study for PAM 0.4 wt% was confirmed.

3.2. Flow Pattern in Two-Phase Flow

Figure 5(a) and Figure 5(b) show the flow pattern map for the test channels upstream and downstream from the expansion in the present experiment. The ordinate and abscissa are the volumetric fluxes of liquid (water and PAM) and air. In the channel upstream, the bubble flow region for the PAM 0.4 wt% aqueous solution is narrower compared to both water and PAM 0.1 wt% aqueous solution. This is due to the higher liquid viscosity, causing thicker liquid film between the bubble slug and the channel wall in the PAM 0.1 wt% aqueous solution than water.

Figures 6(a)-(c) show typical flows in the test channel of air-PAM 0.4 wt% aqueous solution flow, respectively for a bubbly flow at j_GN = 0.1 m/s, j_LN = 0.5 m/s, a slug flow at j_GN = 0.5 m/s, j_LN = 0.5 m/s and an annular flow at j_GN = 10 m/s, j_LN = 0.5 m/s. Three pictures were taken from the top of the channel, respectively at section 1, 2 and 3. After passing through the sudden expansion, the formation of vortex can be seen in figures (b) and (c). By the vortex formation, the energy loss most occur at a region just downstream from the sudden expansion.

3.3. Bubble Velocity and Void Fraction in Two-Phase Flow

Figure 7 shows the bubble velocity data, u_G, in the present experiment against the total volumetric flux of liquid and gas, j (=j_L + j_G). Bubble velocity data for both the narrow channel and the wide channel upstream and downstream from the expansion are simultaneously plotted. The solid line of u_G = j is applicable to homogenous flows. The dashed lines indicates the velocity when all bubbles concentrate at the channel axis in turbulent liquid flow in circular channel, while the dot dash line indicates that when all bubbles concentrate there in laminar liquid flow between parallel flat plates. The highest velocities are recorded by the PAM 0.4 wt% aqueous solution. This is due to the highest viscosity among the three test liquids, causing thicker liquid film between the bubble slugs and the channel wall, and reducing the flow area of the bubbles.

Figure 8 shows a comparison of bubble velocity between experiment and calculation by the drift flux model of Zuber and Findlay [22] , Equation (5), together with Equations (7) and (8). The calculations agree with the data within root mean square errors of 20%.

(5)

Here, the drift velocity, V_Gj was taken as zero because of horizontal flow. The distribution parameter, C₀, was determined based on the microchannel flow data by Kawahara’s correlation [23] .

(6)

Here, Bo is the Bond number, Re_L the liquid Reynolds number and We_G the gas Weber number. Miyagawa et al. [24] modified the distribution parameter, C₀ based on the data for rectangular mini-channel having the hydrodynamic diameters of D_H = 3 mm and 4 mm.

for D_H = 3 mm (7)

for D_H = 4 mm (8)

Figure 9 shows the void fraction data, α, in the present experiment against the gas-phase volume flow rate

fraction,. The solid line of α = β is applicable to homogeneous flow, and the dashed lines

represents the Armand’s correlation [25] ,. The α data for the air-water flows agree reasonably with the calculation by Armand’s correlation [25] , but the data for the present air-PAM 0.4 wt% flows are about 20% lower than those for the air-water flows.

Six correlations developed for macro, mini and micro-channels are examined to validate their suitability against the present void fraction data. Table 3 and Table 4 list the mean error, ε_M, and the RMS error, , for the respective correlations in the upstream and the downstream channel data. The mean error and the RMS error are defined as:

(9)

(10)

Of these, modified Kawahara et al. [29] and Schmidt & Friedel’s correlations [30] give better prediction than others for the narrow channel, while Zhang et al.’s correlation [28] for the wide channel.

3.4. Bubble Length

Figure 10(a) shows the data on the ratio of bubble length to unit cell length L (=L_G + L_L; L_L is the liquid slug length) against the void factor, α. The solid line is calculated by Kanezaki et al.’s correlation [31] applicable to vertical upward air-water flows in 26 mm i.d. pipe.

(11)

Almost all of the experimental data are higher than the solid line and the dashed lines (L_G/L = 1.5α). In addition, the data for the wide channel are higher than those for the narrow channel. Concerning, Kawahara et al. [29] proposed Equation (12) for horizontal two-phase flows in a rectangular microchannel. Where β is the homogeneous void fraction, , Figure 10(b) compares our data to the calculation by Equation (12).

(12)

The data for the wide channel are higher than those for the narrow channel, especially for PAM 0.4 wt% aqueous solution.

3.5. Pressure Change across Expansion

The experiment on the single-phase pressure change at expansion, ∆P_e, are plotted against the mean velocity of liquid in narrow channel, u_LN in Figure 11. ∆P_e for both the water flow and the PAM flow increase with u_LN. This is mainly by the increase in the reversible pressure rise, ∆P_e,R, than the irreversible pressure drop, ∆P_e,I. For PAM 0.4 wt%, ∆P_e were higher than that of water. From the ∆P_e, data the coefficient of the irreversible expansion in single-phase liquid flow, k_e,I, was calculated using Equation (13).

(13)

here,

(14)

The resulting k_e,I data are plotted in Figure 12. The broken line shows the calculation by Borda-Carnot’s formula (=), while the solid line shows the calculation by Miyagawa et al.’s correlation [24] . As seen in the figure, the data on k_e,I gradually approachto the calculation lines with the increase in Re_N, and the data in turbulent for water become almost constant nearby the calculation line by Miyagawa et al.’s correlation [24] .

Figure 13(a) and Figure 13(b) show the present two-phase frictional pressure drop data for the channels upstream and downstream from the expansion, , against the gas volumetric flux, j_G. In general, the pressure gradient increases with the gas volumetric flux, j_G, and the present two-phase frictional pressure drop data for both the channels increase with j_L at a fixed j_G.

Frictional pressure drop data are commonly correlated with the following two-phase friction multiplier, (Lochhart & Martinelli, [32] ):

(15)

where is the frictional pressure drop when the liquid flows alone in the same channel. A widely used correlation for the friction multiplier is that proposed by Chisholm and Laird [33] :

(16)

where X is the Lockhart-Martinelli parameter given by

(17)

In Equation (17), is the frictional pressure drop when the gas flows alone in the same channel.

Figure 14(a) and Figure 14(b) show data against X for the channels upstream and downstream from the expansion. The dashed lines is the calculated curve by the following Mishima-Hibiki’s C correlation [27] :

(18)

where D_H is the hydraulic diameter of the channel in millimeter. The data are well correlated with the Lockhart-Martinelli parameter with the Mishima-Hibiki’s C correlation [27] .

Expansion pressure drop correlations for two-phase flows in literatures are tested against the present data. For evaluating the accuracy in prediction, the following absolute mean and root mean square errors are used.

(19)

(20)

Table 5 lists the and the of six correlations against the present data. Miyagawa et al.’s correlation [24] gives the best prediction. Figures 15(a)-(f) show a comparison of the two-phase pressure change due to the expansion between experiment and calculations. Most of the data could be well predicted by these correlations within 100% in the relative error.

4. Conclusions

Non-Newtonian two-phase flow characteristics across sudden expansion in horizontal rectangular minichannel have been studied experimentally. Main findings are as follows:

1) The two-phase flow patterns were classified into bubble flow, slug flow and annular flow, irrespective of the difference of the test liquid. The bubble flow regime was narrowed in PAM 0.4 wt% case.

2) All the bubble velocity data were higher than that calculated by homogenous flow model, and the highest values were recorded in the PAM 0.4 wt% case. The calculations of bubble velocity by the drift flux model with Miyagawa et al.’s correlation [24] agreed with the present data within root mean square errors of 20%.

3) The void fraction data for the present air-PAM 0.4 wt% flows were about 20% lower than those for the air-water flows. The void fraction data were used to test six correlations in literatures. Modified Kawahara et al.’s [29] and Schmidt & Friedel’s correlations [30] gave better prediction than the others for the narrow channel, while Zhang et al.’s correlation [28] for the wide channel.

4) The bubble length data for both the upstream and the downstream channels were longer for air-PAM flow case than air-water one, especially for PAM 0.4 wt%.

5) The single-phase pressure change data due to expansion, ∆P_e, increased with the mean velocity of liquid in narrow channel, u_LN. The irreversible expansion pressure loss coefficient data, k_e,I, gradually approached to the calculations by Borda-Carnot’s formula and Miyagawa et al.’s correlation for turbulent flow [24] with the increase in Re_N.

6) The two-phase frictional pressure dropin the channels for upstream and downstream from the expansion,

, increased with the gas volumetric fluxand with the liquid volumetric flux.

7) Two-phase friction multiplier data were well correlated with the Lockhart-Martinelli parameter with Mishima-Hibiki’s C correlation [27] .

8) The two-phase expansion pressure drop data were used to test six correlations in literatures, and Miyagawa et al.’s correlation [24] gave the best prediction.

Acknowledgements

The authors deeply appreciate DIKTI of Indonesian government and State Polytechnic of Cilacap for the fel-

lowship and the permission to Mr. Agus Santoso to study in Kumamoto University. Appreciation is also to Mr. Miyagawa for his fruitful discussions and advise.

Conflicts of Interest

The authors declare no conflicts of interest.

References